| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- kubeflow
- 강화학습
- 데이터마이닝
- 신경망
- 인공지능
- 기계학습
- 쿠브플로우
- hadoop
- 하둡
- 논문리뷰
- 신경망학습
- Spark
- 파이토치
- 도커
- dockerfile
- 딥러닝
- 분산처리
- Kubenetes
- 활성화함수
- 하둡에코시스템
- 도커파일
- 쿠버네티스
- 뉴럴네트워크
- 머신러닝
- ResNet
- 스파크
- CNN
- docker
- VGGNet
- 빅데이터
Archives
- Today
- Total
Daily training log
Graph Neural Networks 본문
Graph Representation Learning (GRL)
- Node Embedding : node의 구조나 피쳐를 잘 조합해서 Feature Vector로 매핑하는 것을 의미
- Graph Task
- Node level : Node의 종류 예측, 분류
- Edge level : Node 사이의 Edge가 존재하냐
- Graph level : Graph 자체를 분류, Graph가 다음에 어떻게 바뀔 것인지 prediction
- 응용
- 구글의 AlphaFold
- 추천 시스템
- AI 신약 개발
- 비전에서 Scene Graph 생성
- Scene Graph으로부터 이미지 생성
- Knowledge Graph
Graph

- Node와, Node 사이를 이어주는 Edge로 구성됨.
- Node의 Feature를 어떻게 쓸건지, Graph 자체의 Adjacency Matix를 어떻게 쓸건지 초점을 맞춤
- 위와 같은 그래프를 Homogeneous라고 함
Heterogeneous graph

- Node의 종류가 다름.
- 같은 type의 Node는 Edge가 없음. 위에서는 3 C 2개의 Edge 종류
Node Embedding

- 비슷한 Node는 Embedding space에 가깝게 위치시키기
- Encoder function과 원래 Graph의 Similarity fuction을 정의해야 됨
Node의 유사도를 어떻게 정의할 것인가

- Node level
- Degree로 정의
- Clustering coefficient로 정의 : 이웃하는 Node들이 연결되어 있는지


- Edge level
- Local neighborhood overlap : 이웃들이 얼마나 겹치는지
- common neighbors : 단순 겹치는 것 계산, But Degree의 영향을 받을 수 있음
=> Jacarrd, Adamic-Adar 등으로도 계산할 수 있음 - Random-walk based : Non-deterministic하게 계산
- common neighbors : 단순 겹치는 것 계산, But Degree의 영향을 받을 수 있음
- Local neighborhood overlap : 이웃들이 얼마나 겹치는지
Encoder를 어떻게 정의할 것인가

- Shallow embedding : 제일 단순하게는 One-Hot vector를 학습함 => Encoder가 Vector를 look-up하는 방식
- 단점
- 너무 많은 파라미터를 학습해야 함
- Transductive 함 (새롭게 나오는 Unseen node를 학습하지 못함) <=> Inductive
- 단점
- GNN의 등장
Graph Neural Network (GNN)


- Neural Network를 거쳐서 Hidden representation을 생성함
- Convolution
- Graph는 Grid Structure가 아니라 비전의 CNN 같이 Sliding window를 정의할 수 없음
Message Passing NNs (MPNN)

- GNN에서 제일 중요한 파트
- 자기 이웃들로부터 Message 라는 정보를 받아서 학습을 하겠음
- A의 노드 정보를 학습하기 위해, 연결되어 있는 B, C, D의 정보를 잘 연결해줘야 됨 / 두가지 파트로 구성
- Message Passing (Aggregation) : 이웃으로부터 합쳐서 정보를 받아옴
- Update : 메세지로부터 자신의 Hidden state를 업데이트 함


- h : hidden representation, h^{t+1} : 일종의 레이어
- N : neighborhood, v 기준으로 메세지를 보고 있음
- 위 예시에서는 Sum으로 Aggregate하고 있음
- B, C, D를 합쳐서 A한테 메세지를 보냄 // 자신의 t Rep와 메세지를 합쳐서 t+1 Rep를 만듦
- 최종적으로 y hat이라는 Representation vector를 얻어냄

- 메세지 패싱 구조에 NN을 붙이는 게 GNN의 목적
- 위의 예시에서는 Update fuction에 Linear layer 라고 붙임 => 가장 기초적인 GNN
- Node의 Feature와 함께, 임의의 detph를 가진 이웃의 정보를 같이 가져올 수 있음
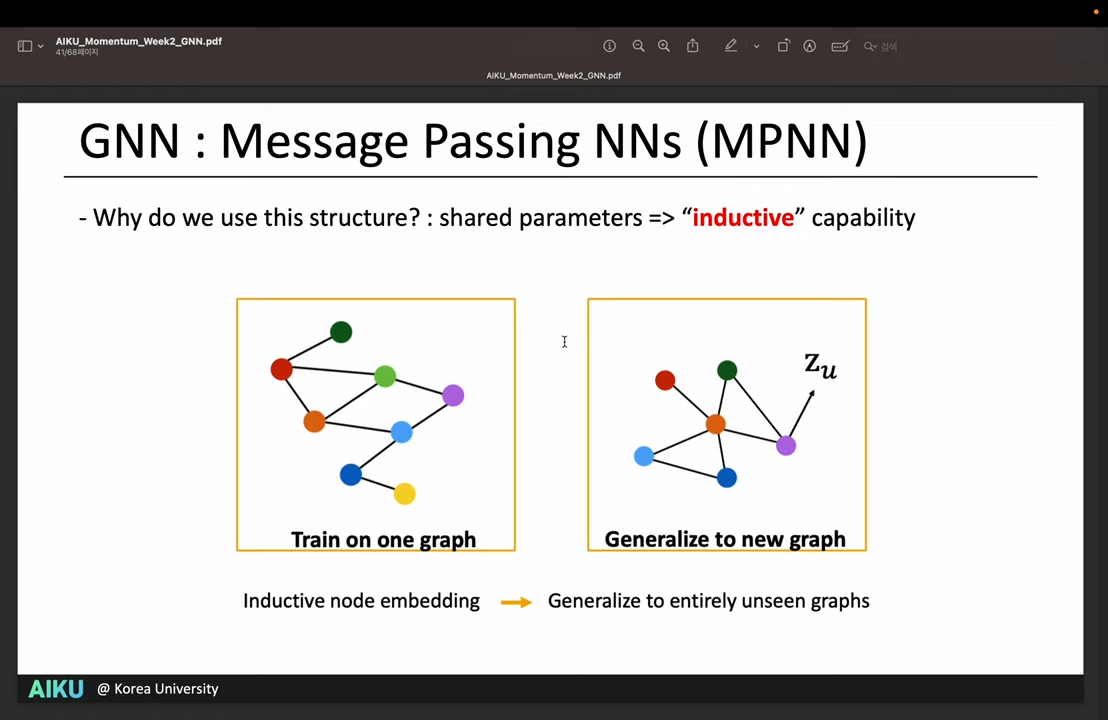
- 모든 Node에 대해 같은 Parameter를 학습하기 때문에, Inductive capability를 얻을 수 있음
- 새로운 Node가 생겨도 일반화가 가능함
Loss function

- Contrastive learning 에서 쓰이는 것처럼, 비슷한 Node는 비슷한 Embedding을 가지도록 학습
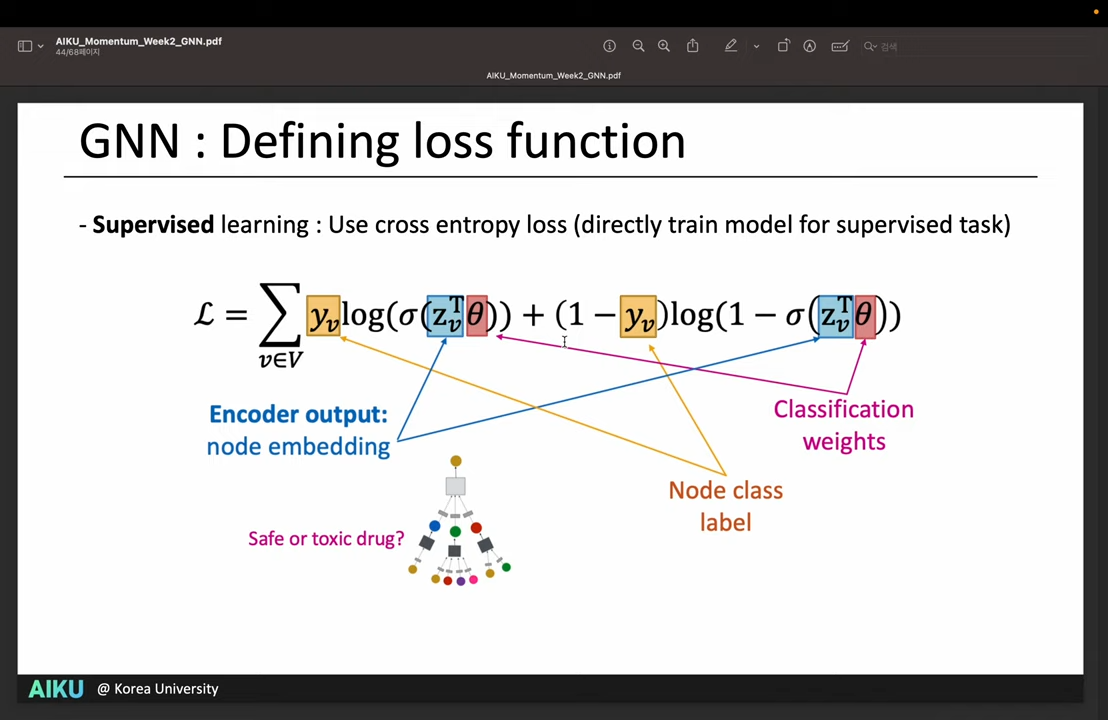
- Supervised learning처럼 CE 사용 가능
- But 위와 같은 방법은 Node의 Degree에 굉장히 민감해짐.
- A 노드가 B 노드에 비해 이웃이 100배 많으면, 너무 큰 노드(A)로 쏠려버림 (Oversmoothing)
- 레이어를 조금만 깊게 쌓아도 (4~5개) 이러한 문제가 발생함
- 가장 단순하게 Normalization 해서 위의 문제를 해결할 수 있음
Graph Convolutional Network



- symmetric-normalization : 자기 이웃들의 Degree를 고려하여 Aggregation passing을 Normalization함
- self-loop update : aggregation function에 자기 자신을 합쳐서 효율적으로 update 함
- 수식은 직접 논문 참고
- But, 모든 Node와 Degree를 참고해야 되기 때문에 엄밀하게는 Inductive setting이 아님
GraphSAGE
- Neighborhood를 샘플링 (Random walk) 해서 Inductive setting
- Aggregate 방식은 위와 똑같음
- 세가지 방식 (Mean, Pool, LSTM) 을 제시해서 관찰함


- Negative sampling : Random walk 상에서 같이 등장하지 않을 likelihood를 빼줌
- Node 들의 feature를 학습하면, Graph의 Structure를 보여줄 수 있음
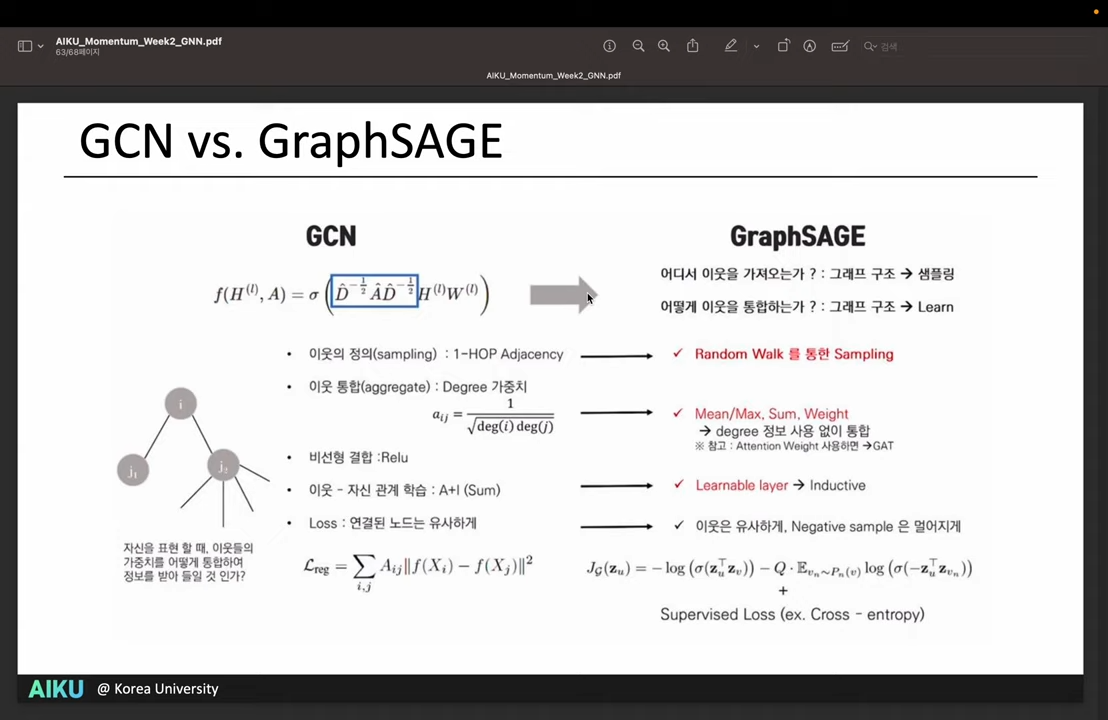
- 이후 연구는 Attention, Transformer 구조를 GNN에 적용하려고 함
참고 자료
'Base' 카테고리의 다른 글
| Scene Graph Generation (0) | 2024.07.10 |
|---|
Comments

